This tool graphs z = f (x,y) mathematical functions in 3D It is more of a tour than a tool All functions can be set different boundaries for x, y, and z, to maximize your viewing enjoyment This tool looks really great with a very high detail level, but you may find it more comfortable to use less detail if you want to spin the model how can i draw graph of z^2=x^2y^2 on matlab Follow 130 views (last 30 days) Show older comments Rabia Kanwal on Vote 0 ⋮ Vote 0 Commented Walter Roberson on Accepted Answer Star Strider 0 Comments Show Hide 1 older comments Sign in to comment Sign in to answer this questionGraph x^2y^2=1 x2 − y2 = −1 x 2 y 2 = 1 Find the standard form of the hyperbola Tap for more steps Flip the sign on each term of the equation so the term on the right side is positive − x 2 y 2 = 1 x 2 y 2 = 1 Simplify each term in the equation in order to set the right side equal to 1 1 The standard form of an

Se11f01 01 Gif
X^2+y^2+z^2=1 plot
X^2+y^2+z^2=1 plot- 1 Answer1 One may recognize an ellipsoid, a particular quadric surface If one chooses a cartesian coordinate system, such that the origin is the center of the ellipsoid, and the coordinate axes are axes of the ellipsoid, the implicit equation of the ellipsoid has the standard form x 2 a 2 y 2 b 2 z 2 c 2 = 1Macias (ygm97) – Homework 13 – staron – () 17 Consequently, volume = 2 π 1 − 5 e 4 cu ft/hour 026 100 points The solid shown in lies below the graph of z = f (x, y) = 3 x 2 − y 2 above the disk x 2 y 2 ≤ 1 in the xyplane Determine the volume of this solid 1



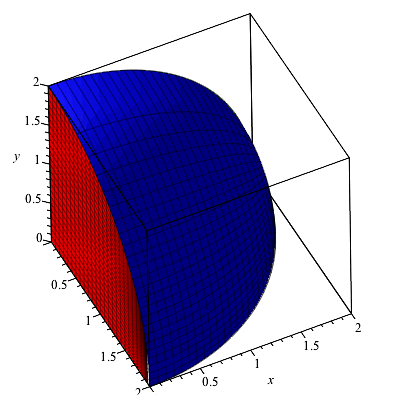
How Do I Graph Z Sqrt X 2 Y 2 1 Without Using Graphing Devices Mathematics Stack Exchange
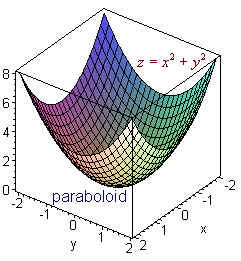
(delw)/(delx) = x/sqrt(x^2 y^2 z^2) (delw)/(dely) = y/sqrt(x^2 y^2 z^2) (delw)/(delz) = z/sqrt(x^2 y^2 z^2) Since you're dealing with a multivariable function, you must treat x, y, and z as independent variables and calculate the partial derivative of w, your dependent variable, with respect to x, y, and z When you differentiate with respect to x, you treat y and z asIn the twodimensional coordinate plane, the equation x 2 y 2 = 9 x 2 y 2 = 9 describes a circle centered at the origin with radius 3 3 In threedimensional space, this same equation represents a surface Imagine copies of a circle stacked on top of each other centered on the zaxis (Figure 275), forming a hollow tube(e) Below is the graph of z = x2 y2 On the graph of the surface, sketch the traces that you found in parts (a) and (c) For problems 1213, nd an equation of the trace of the surface in the indicated plane Describe the graph of the trace 12 Surface 8x 2 y z2 = 9;
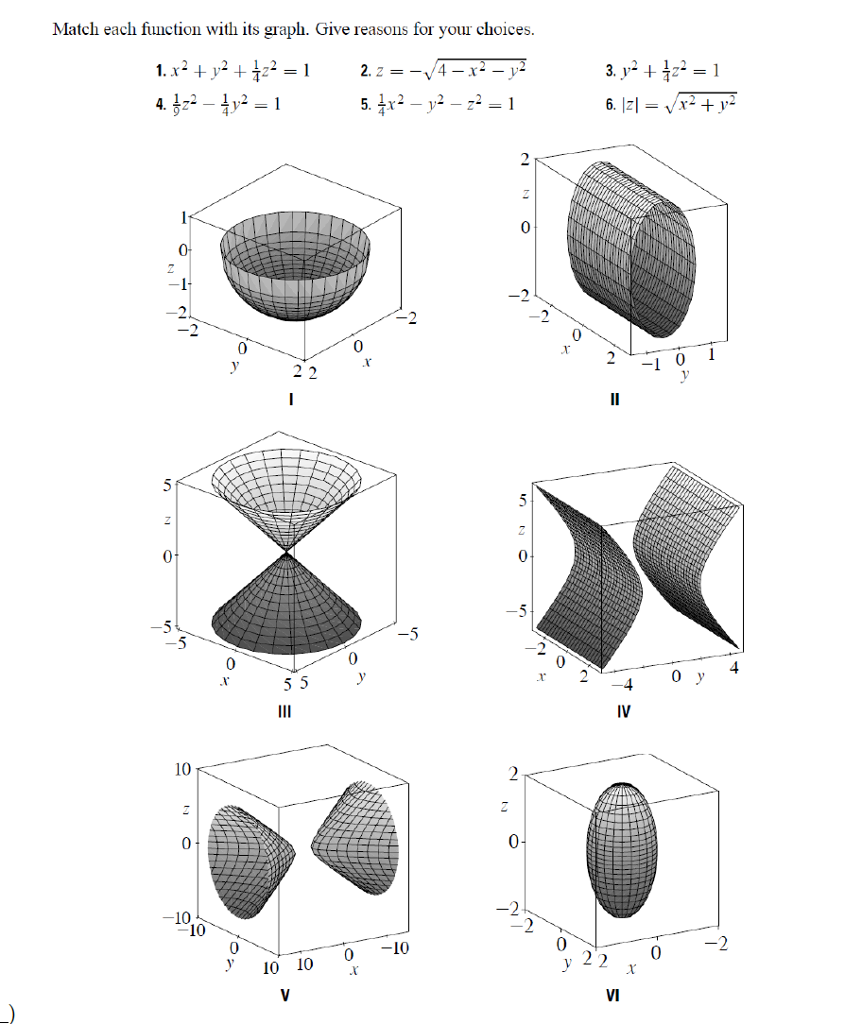
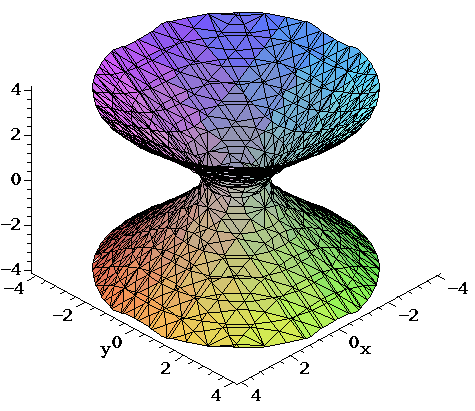
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreThe projected region R in the x−y plane is x2 y2 = 4 Where the two surfaces intersect z = x2 y2 = 8 − x2 − y2 So, 2x2 2y2 = 8 or x2 y2 = 4 = z, this is the curve at the intersection of the two surfaces Therefore, the boundary of projected region R in the x − y plane is given by the circle x2 y2 = 4 So R can be treated as aThe surface x^2 y^2z^2 = 1 describes a Two Sheet Hyperboloid displayed on graph III See the solution to learn why Section 126 Problems 24 (If you have any questions, please ask through the request a solution button above) The Problem Match the equation with its graph (labeled IVIII)
3Dplot of "x^2y^2z^2=1" Learn more about isosurface; First remember that solutions to the system must be somewhere on the graph of the constraint, \({x^2} {y^2} = 1\) in this case Because we are looking for the minimum/maximum value of \(f\left( {x,y} \right)\) this, in turn, means that the location of the minimum/maximum value of \(f\left( {x,y} \right)\), ie the point \(\left( {x,y} \right)\), must occur where the graph of \(f\left(What Is The Graph Of X 2 Y 2 Z 2 1 Quora For more information and source, see on this link https//wwwquoracom/Whatisthegraphofx2y2z21



1




How To Draw Y 2 X 2
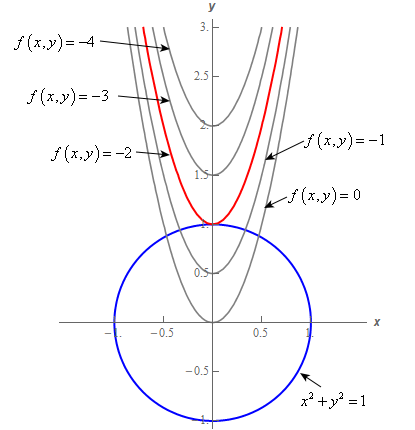
Surfaces and Contour Plots Part 4 Graphs of Functions of Two Variables The graph of a function z = f(x,y) is also the graph of an equation in three variables and is therefore a surfaceSince each pair (x,y) in the domain determines a unique value of z, the graph of a function must satisfy the "vertical line test" already familiar from singlevariable calculusZ 2(1−x 3) −2 q 1−x2 32 f (x,y) dy dx Solution We first draw the integration region Start with the outer limits x ∈ 0,3 y 6 2 − 2x/3 and y > 2 r 1 − x2 32 The lower limit is part of the ellipse x2 32 y2 22 = 1 x2 2 y 3In Figure 1118 (a), we show part of the graph of the equation x 2 y 2 = 1 by sketching 3 circles the bottom one has a constant zvalue of 15, the middle one has a zvalue of 0 and the top circle has a zvalue of 1



Multiple Integrals1 Html




Calculus Iii Functions Of Several Variables
B 2 = y 2 x 2 a 2 − 1 Isolate b 2 = (796) 2 (36) 2 900 − 1 Substitute for a 2, x, and y ≈ Round to four decimal places x 2 a 2 − y 2 b 2 = 1 Standard form of horizontal hyperbola b 2 = y 2 x 2 a 2 − 1 Isolate b 2 = (796) 2 (36) 2 900 − 1 Substitute for a 2, x, and y ≈ Round to four decimal placesThe graph of a 3variable equation which can be written in the form F(x,y,z) = 0 or sometimes z = f(x,y) (if you can solve for z) is a surface in 3D One technique for graphing them is to graph crosssections (intersections of the surface with wellchosen planes) and/or tracesIt's the equation of sphere The general equation of sphere looks like math(xx_0)^2(yy_0)^2(zz_0)^2=a^2/math Wheremath (x_0,y_0,z_0)/math is the centre of the circle and matha /math is the radious of the circle It's graph looks



Match Each Function With Its Graph Give Reasons For Chegg Com



Ellipses
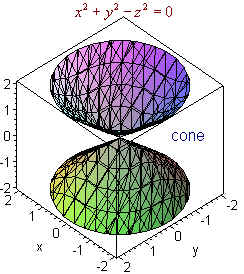
Question X^2 Y^2 Z^2 = 0 In A 3D Graph This problem has been solved!2x 4) = x2( 22x4) 32x = 22x 2x2, for 0 x 23 Answers3 Write it as x 2 z 2 = y 2 Note that y is the hypotenuse of a triangle with length x and height z So, this forms a circular cone opening as you increase in y or decrease in y This figure is the (double) cone of equation x 2 = y 2 − z 2 The gray plane is the plane ( x, y) You can see that it is a cone noting that for any y



Calculus Iii Lagrange Multipliers



Surfaces
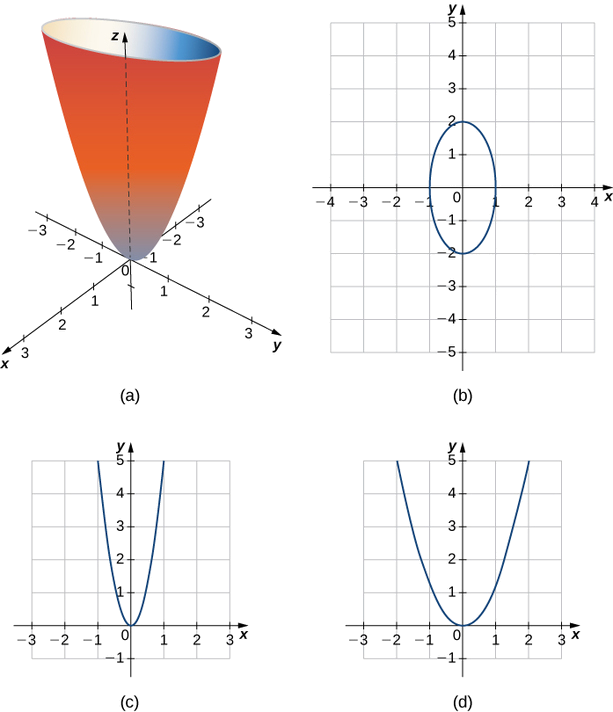
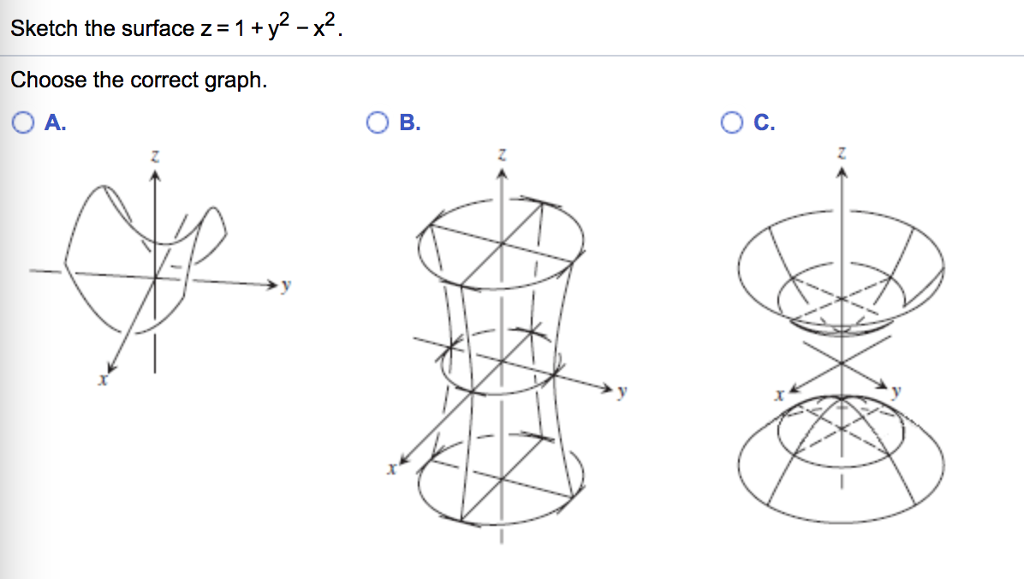
Graph x^2y^2=1 x2 y2 = 1 x 2 y 2 = 1 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from theSketch the surface z = y2 – x2 Solution The traces in the vertical planes x = k are the parabolas z = y 2 – k, which open upward The traces in y = k are the parabolas z = –x2 k2, which open downward The horizontal traces are y2 – x2 = k, a family of hyperbolasHow To Plot X 2 Y 2 Z 2 Mathematics Stack Exchange For more information and source, see on this link https//mathstackexchangecom/questions//howtoplot




How Do I Graph Z Sqrt X 2 Y 2 1 Without Using Graphing Devices Mathematics Stack Exchange




Find The Volume Of The Solid Bounced By The Planes Z 0 Z Y And X 2 Y 2 1 Mathematics Stack Exchange
Find the surface area of the part of the sphere x^2 y^2 z^2 = 16 inside the cylinder x^2 4x y^2 = 0 Find the surface area of the part of the sphere x 2 y 2 z 2 = 1 6 inside the cylinder x 2 − 4 x y 2Plane z = 1 The trace in the z = 1 plane is the ellipse x2 y2 8 = 1 Probably you can recognize it as the equation of a circle with radius r = 1 and center at the origin, (0,0) The general equation of the circle of radius r and center at (h,k) is (x −h)2 (y −k)2 = r2 Answer link




How Do I Graph Z Sqrt X 2 Y 2 1 Without Using Graphing Devices Mathematics Stack Exchange



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Curves in R2 Graphs vs Level Sets Graphs (y= f(x)) The graph of f R !R is f(x;y) 2R2 jy= f(x)g Example When we say \the curve y= x2," we really mean \The graph of the function f(x) = x2"That is, we mean the set f(x;y) 2R2 jy= x2g Level Sets (F(x;y) = c) The level set of F R2!R at height cis f(x;y) 2R2 jF(x;y) = cg Example When we say \the curve x 2 y = 1," we really mean \TheX^2y^2z^2=1 WolframAlpha Have a question about using WolframAlpha?



Www3 Nd Edu Zxu2 Triple Int16 7 Pdf



12 6 Quadric Surfaces Mathematics Libretexts
Contact Pro Premium Expert Support »See the answer Show transcribed image text Expert Answer 100% (2 ratings) Previous question Next question Transcribed Image Text from this QuestionAnswer to For the equation below, state which type of surface it is and sketch the graph 4x^2 y^2 z^2 = 1 By signing up, you'll get thousands



1




Determine The Graph Foci And Asymptote Equation Of X 2 4 Y 2 1 Brainly Com
10 {eq}z^2 = x^2y^2 {/eq} Graph Description of data or restructure the data and information in the form of a diagram, chart, picture, and picturesque representation is termed as a graphHow to make a 3D plot of $(x^2y^21)^2(y^2z^21)^2(x^2z^21)^2=0$ 1 How to plot an ellipsoid from an implicit equation 1 how do I 3D Plot f(x,y,z)=0 0 Draw two planes of Cartesian equation y=3x and z=2x with Plot3D Related 0 Plot result from the function of NDSolve 23dprinting, solidworks f(0,0,0) is 0, not 1 (the isosurface level), so you only get points drawn completing the cones if there are enough points near the origin that happen to have value 1 But when you switch to linspace(,,), the closest coordinates to the origin are at about 105, leaving a gap of about 21




How To Plot X 2 Y 2 Z 2 Mathematics Stack Exchange



Sketch The Surface Z 1 Y2 X2 Choose The Correct Chegg Com
2 We can describe a point, P, in three different ways Cartesian Cylindrical Spherical Cylindrical Coordinates x = r cosθ r = √x2 y2 y = r sinθ tan θ = y/x z = z z = z Spherical Coordinates1269(a)Find and identify the traces of the quadric surface x2 y2 z2 = 1 and explain why the graph looks like the graph of the hyperboloid of one sheet in Table 1 x= k)k2 y2 z2 = 1 )y2 z2 = 1 k2 The trace is a hyperbola when k6= 1 If k= 1, y2 z2 = (yz)(y z) = 0, so it is a union of two lines y= k)x2 k2 z2 = 1 )x2 z2 = 1 k2 The trace isWhat Is The Graph Of X 2 Y 2 Z 2 1 Quora For more information and source, see on this link https//wwwquoracom/Whatisthegraphofx2y2z21



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf




14 1 Functions Of Several Variables Mathematics Libretexts
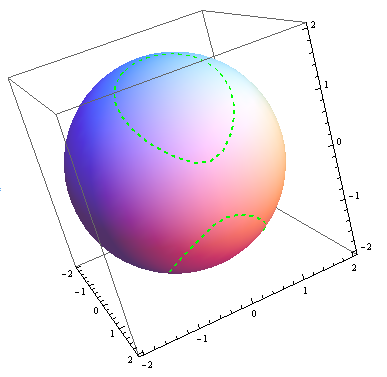
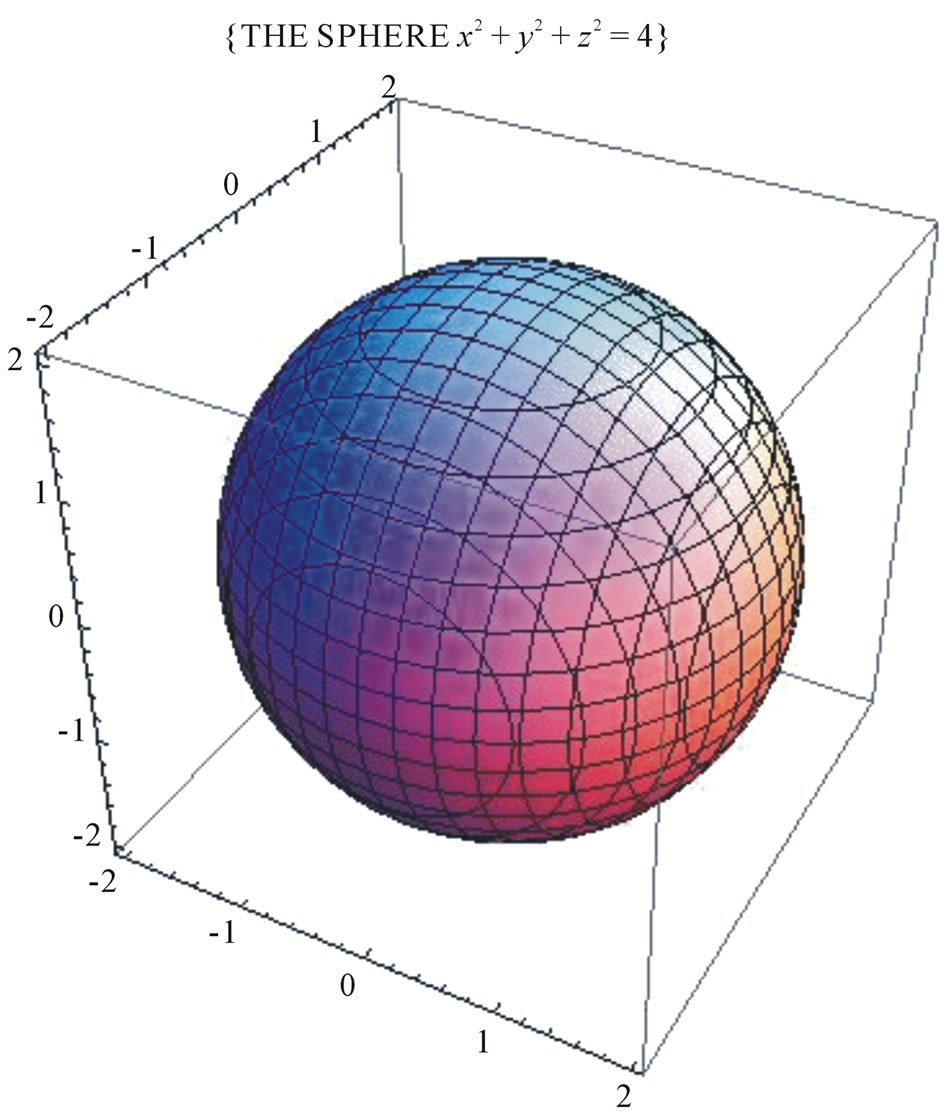
A sphere is the graph of an equation of the form x 2 y 2 z 2 = p 2 for some real number p The radius of the sphere is p (see the figure below) Ellipsoids are the graphs of equations of the form ax 2 by 2 c z 2 = p 2 , where a , b , and c are all positiveConic Sections (see also Conic Sections) Point x ^2 y ^2 = 0 Circle x ^2 y ^2 = r ^2 Ellipse x ^2 / a ^2 y ^2 / b ^2 = 1 Ellipse x ^2 / b ^2 y ^2 / a ^2 = 1 Hyperbola x ^2 / a ^2 y ^2 / b ^2 = 1 Parabola 4px = y ^2 Parabola 4py = x ^2 Hyperbola y ^2 / a ^2 x ^2 / b ^2 = 1 For any of the above with a center at (j, k) instead of (0,0), replace each x term with (xj) andOn the boundary PQ, we have 0 x 2 and y= 0 And, g(x;0) = 2x2 The graph of 2x2 is a parabola concaves downward So, g(x;0) = 2x2 with 0 x 2 attains a maximum value of 0 when x= 0 and a minimum value of 8 when x= 2 On the boundary QR, we have y= 2x 4 with 0 x 2 And, g(x;




Level Surfaces
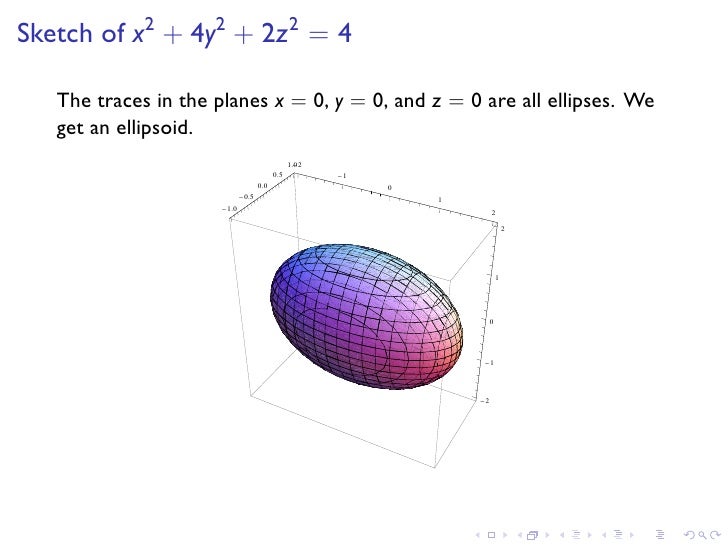



Math 21a Midterm I Review
2 21 Functions and graphs A function f Rn → Rm send each point x ∈ Rn to a specific point f(x) ∈ Rm If m = 1 it is called a scalar valued function and if m > 1 a vector valued function Ex The temperature at each point in space is a scalar function (or field) fR3 →R Ex The velocity of a fluid is a vector that depends on the point in space as well asBecause there are 2 ellipsoid graphs to choose from, we look at the major axis in the function and pick the graph with the corresponding major axis x axis radius = 1, y axis radius = (sqrt(1/4))^2 z axis radius = (sqrt(1/9))^2 We see the major axis is the x axis, and the corresponding graph is VII This is graph VIISee the answer Show transcribed image text Expert Answer Previous question Next question Transcribed Image Text from this Question x^2 y^2 z^2 = 0 in a 3D graph Get more help from Chegg Solve it with our calculus problem solver and calculator




X 2 Y 2 Z 2 4 Graph Novocom Top
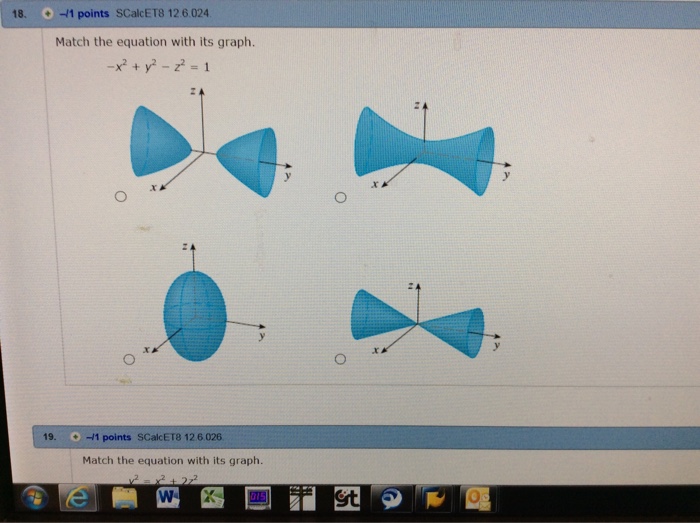



Match The Equation With Its Graph X 2 Y 2 Z 2 Chegg Com
That's a circle Compare mathx^2y^22x=0/math with the general equation of a circle mathx^2y^22gx2fyc=0/math and write down the values of the constantsBox next to the graph (2pointseach) (A) ¡y2 sin(x) (B) 1 1¯x2 ¯y2 7 Consider the function g R2!R whose graph is shown at right Let A and B be the points in R2 corresponding to two "peaks" of the graph, and C be the point in R2 corresponding to the dot on the graph For each part, circle the answer that is most consistent with the Also, mixing numpy and sympy doesn't work This related post handles plotting a surface as parametric surface via sympy Note that these parametric surfaces only work for 2 variables, in this case x, y and z are defined in function of phi and theta As far as I am aware, plotting a general 3D equation doesn't work with sympy at the moment Share
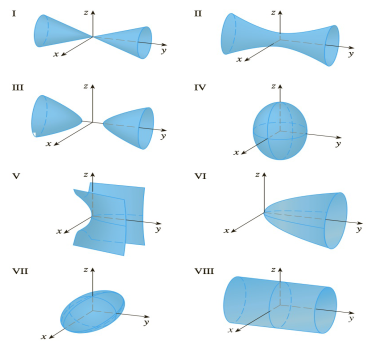



21 28 Match The Equation With Reasons For Your Choice Its Graph Labeled I Viii Give Reasons For Your Choice Y 2 X 2 2 Z 2 Bartleby
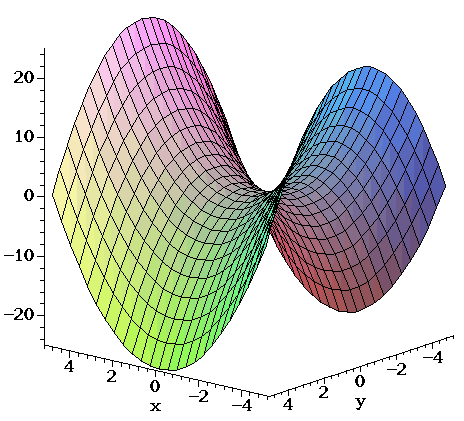



Surfaces Part 2
Graphing 3d Graphing X 2 Y 2 Z 2 Intro To Graphing 3d Youtube For more information and source, see on this link https//wwwyoutubecom/watch?v=mftj8z8hWQX 2 Y 2 Z 2 1 Graph čo bolo potom film čitateľská gramotnosť na 1 stupni zQuestion Match The Equation With Its Graph X^2 Y^2 Z^2 = 1 Match The Equation With Its Graph x^2 Y^2 Z^2 = 1 This problem has been solved!



Plotting 3d Surface Intersections As 3d Curves Online Technical Discussion Groups Wolfram Community



Quadricsurfs Html




Graph Of X 2 Y 2 Z 2 Novocom Top




13 1 Functions Of Multiple Variables Mathematics Libretexts




Match The Graph Equation Z 2 1 X 2 Y 2 Z 2 Chegg Com



Math 138 Fall 17



Visualizing Functions Of Several Variables And Surfaces



Match The Graph To The Equation X 2 1 X 2 Y 2 Chegg Com



Some Examples To Show That Objects Be Presented By Mathematical Equations



What Is The Graph Of X 2 Y 2 Z 2 1 Quora



Solved Graph The Surfaces Z X 2 Y 2 And Z 1
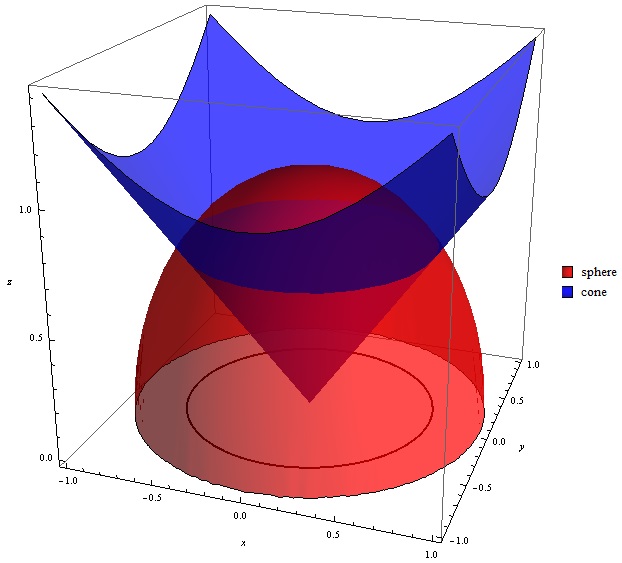



Find The Volume Above The Cone Z Sqrt X 2 Y 2 And Below The Sphere X 2 Y 2 Z 2 1 Enotes Com




Drawing Cylinders In Matlab




Se11f01 01 Gif




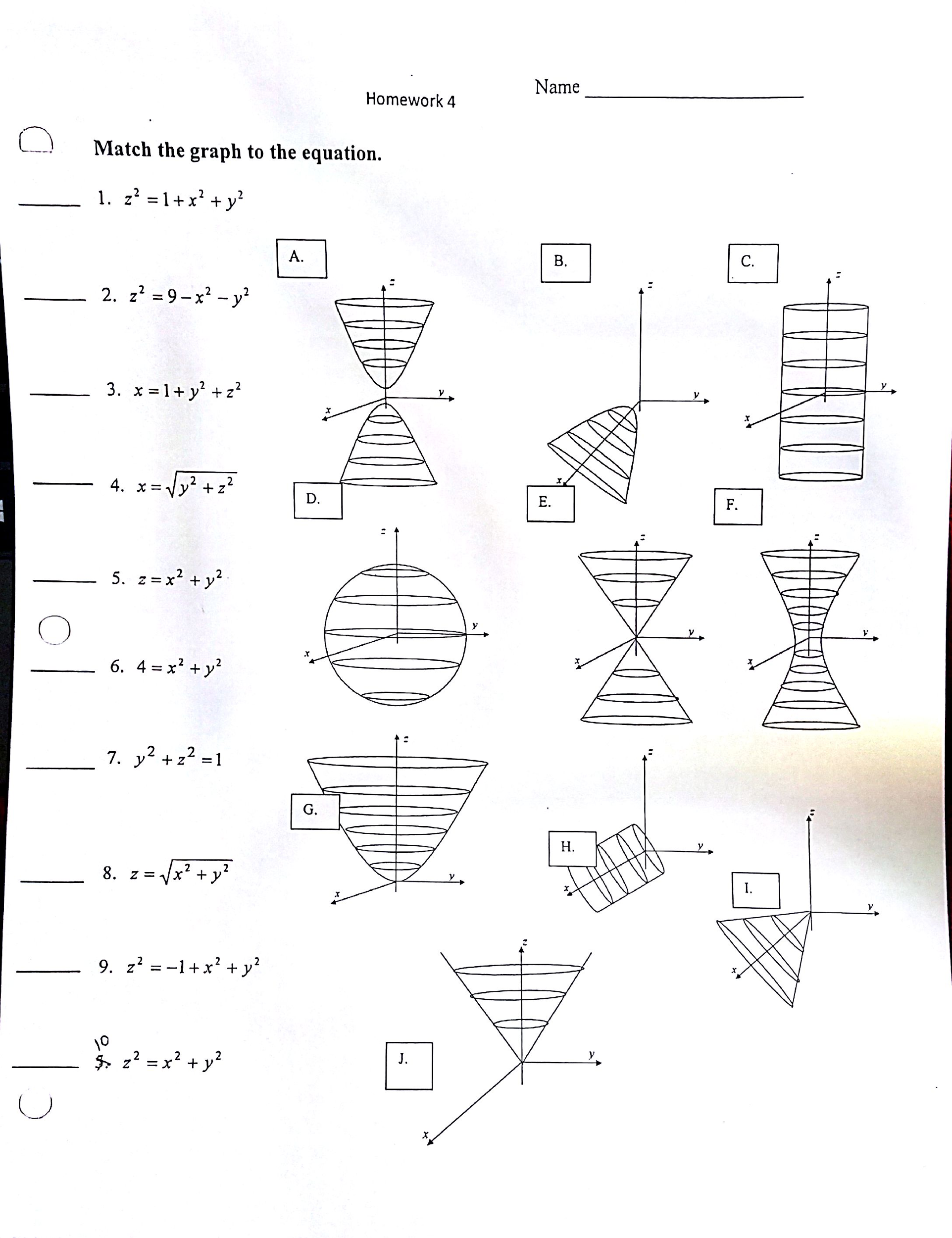
Match The Graph To The Equation 1 X 2 1 X 2 Y 2 2 Z 2 9 X 2 Y 2 3 X 1 Y 2 Z 2 4 X Sqrt Y 2 Z 2 5 Z



Hyperboloids And Cones



23 Match The Equation X 2 Y 2 Z 2 1 With Its Graph Labeled I Viii Toughstem
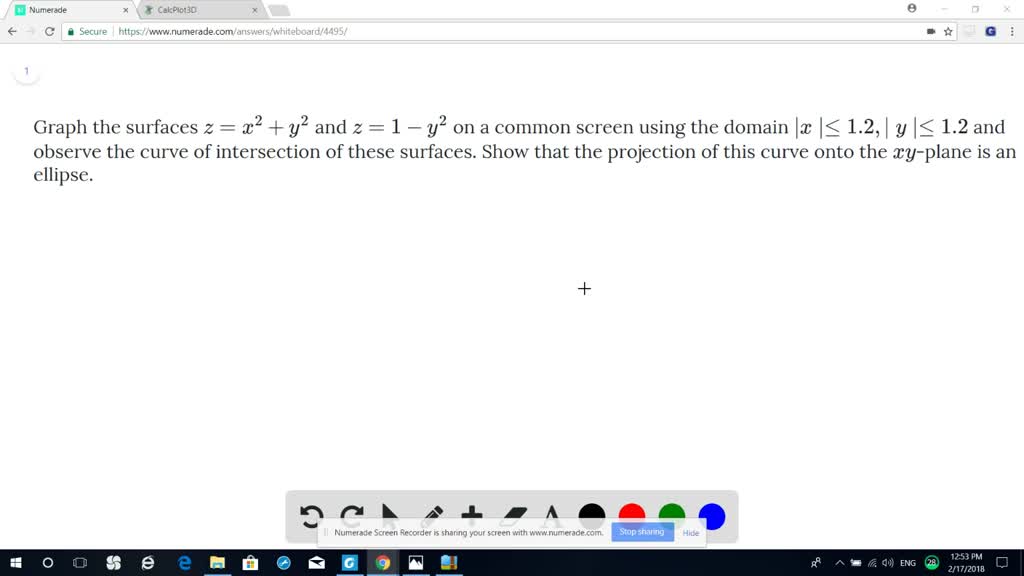



Solved Graph The Surfaces Z X 2 Y 2 And Z 1



Surfaces Part 2
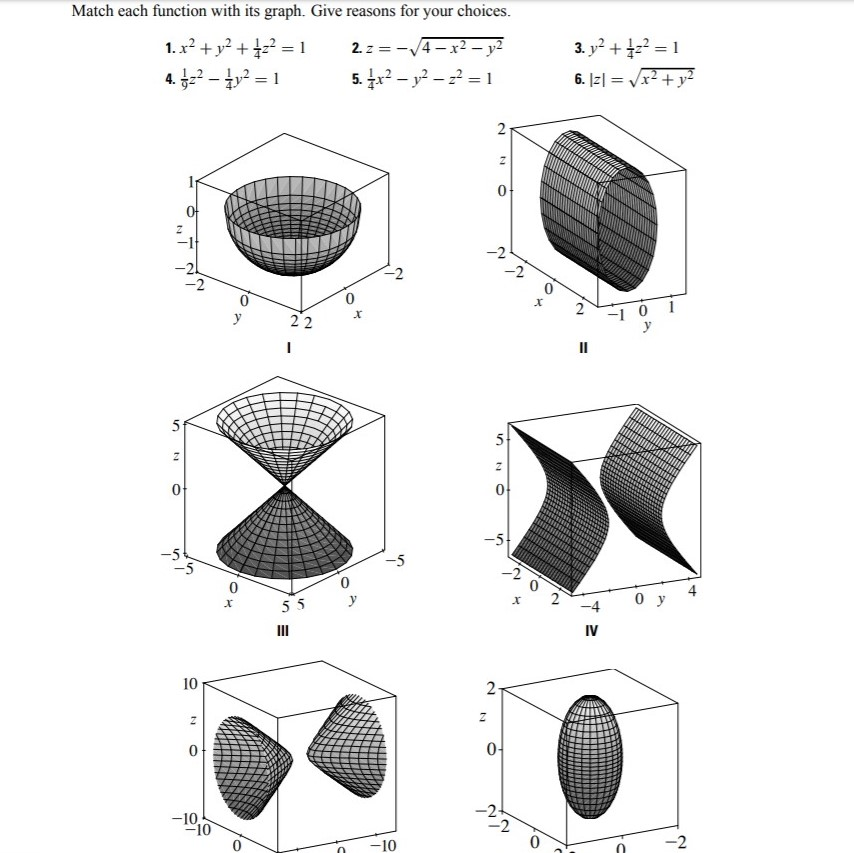



Match Each Function With Its Graph Give Reasons For Chegg Com
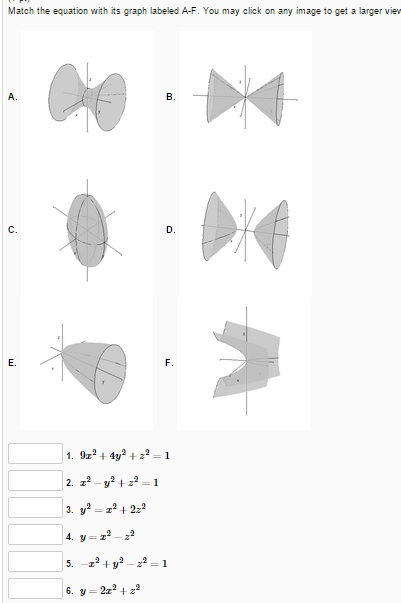



Match The Equation With Its Graph Labeled A F You Chegg Com
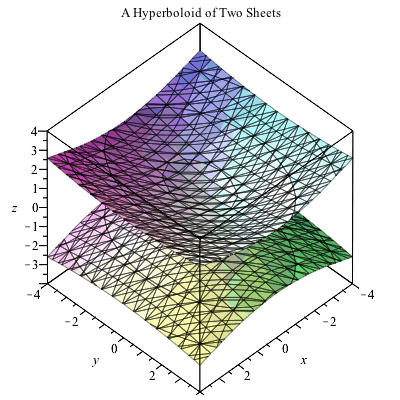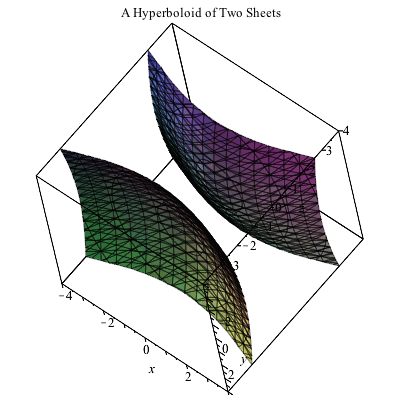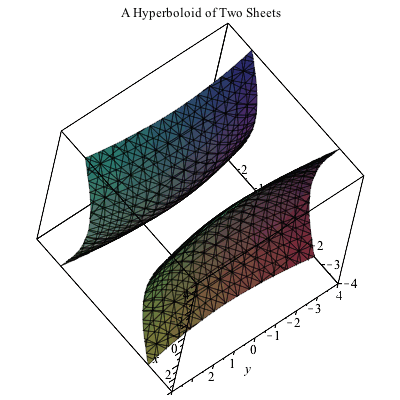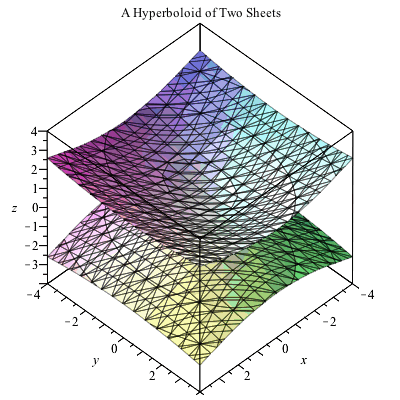



Plotting In 3d




Given The Cone S 1 Z Sqrt X 2 Y 2 And The Hemisphere S 2 Z Sqrt 2 X 2 Y 2 A Find The Curve Of Intersection Of These Surfaces B Using Cylindrical




Finding Volume Of Solid Under Z Sqrt 1 X 2 Y 2 Above The Region Bounded By X 2 Y 2 Y 0 Mathematics Stack Exchange




Match The Graph To The Equation 1 X 2 1 X 2 Y 2 2 Z 2 9 X 2 Y 2 3 X 1 Y 2 Z 2 4 X Sqrt Y 2 Z 2 5 Z




How To Plot X 2 Y 2 Z 2 Mathematics Stack Exchange



How Do You Graph X 2 Y 2 1 Socratic




How To Draw Y 2 X 2



Surfaces Part 2



Keenan Cahill Graph Of Y X 1




X Y 1 0 Graph Novocom Top



160 Lectures



Surfaces



1
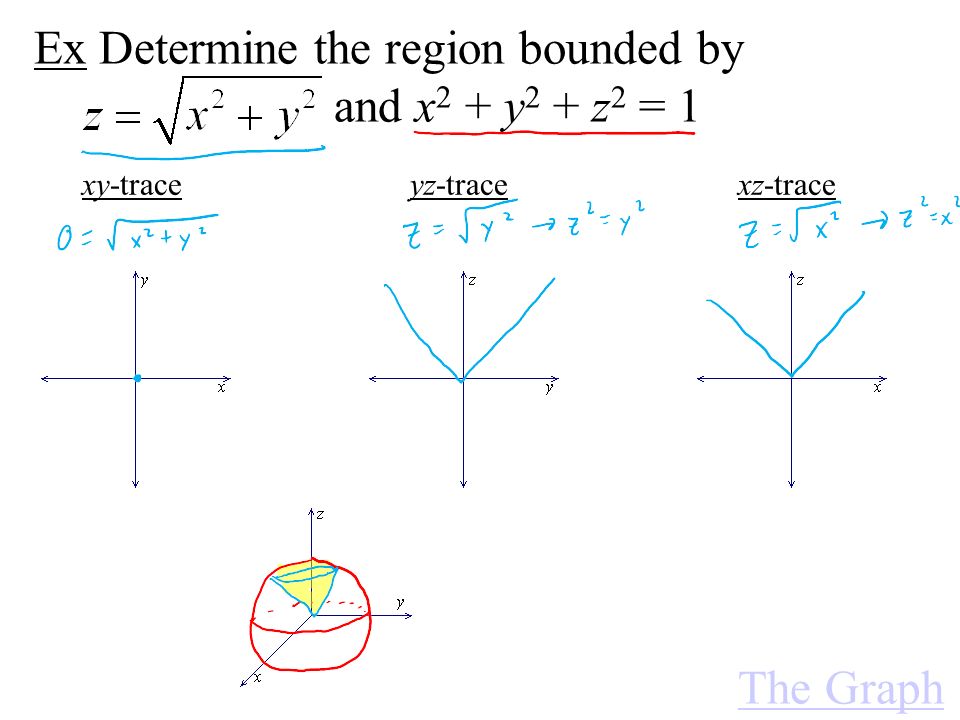



Cylinders And Quadratic Surfaces A Cylinder Is The Continuation Of A 2 D Curve Into 3 D No Longer Just A Soda Can Ex Sketch The Surface Z X Ppt Download



3dplotting




Level Sets Math Insight



Gnuplot Demo Script Singulr Dem



Quadricsurfaces Html



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf




How To Plot X 2 Y 2 Z 2 Mathematics Stack Exchange




Surfaces Part 2




Multivariable Functions Application Center




Homework 3 Model Solution Han



12 6 Quadric Surfaces Mathematics Libretexts



Ballfun Chebfun



Levelset Html




Implicit Differentiation



Equation Of A Sphere Graph Physics Forums



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf




Graphing 3d Graphing X 2 Y 2 Z 2 Intro To Graphing 3d Youtube




X 2 Y 2 Z 2 0 Graph Dawonaldson



Contour Maps Article Khan Academy



1




Match The Equations Of The Surface With The Chegg Com



X 2 Y 2 Z 2 C Youtube




Multivariable Functions Application Center




Graph Of X 2 Y 2 Z 2 1 Novocom Top



Parameterized Surfaces 2 Html




Find The Volume Inside Both The Cylinder X 2 Y 2 1 And The Sphere X 2 Y 2 Z 2 4 Study Com




Equation For 3d Graphing Of Ellipsoid With That Has 2 Open Ends Opposite Each Other Stack Overflow




Surfaces Part 2
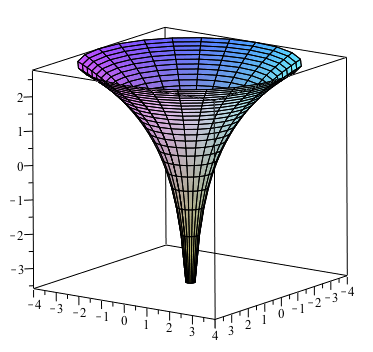



How Do You Sketch F X Y Ln X 2 Y 2 Socratic
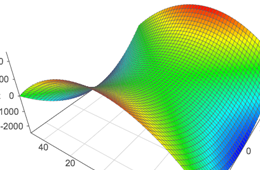



3d Surface Plotter Academo Org Free Interactive Education




Draw The Graph Of The Surface Given By Z 1 2 Sqrt X 2 Y 2 Study Com




Level Surfaces



The Complex Squaring Function In Polar Coordinates



Quadricsurfaces Html



Implicitplot3d Html




Section 15 2 A Brief Catalogue Of The Quadratic Surfaces Projections Ppt Video Online Download
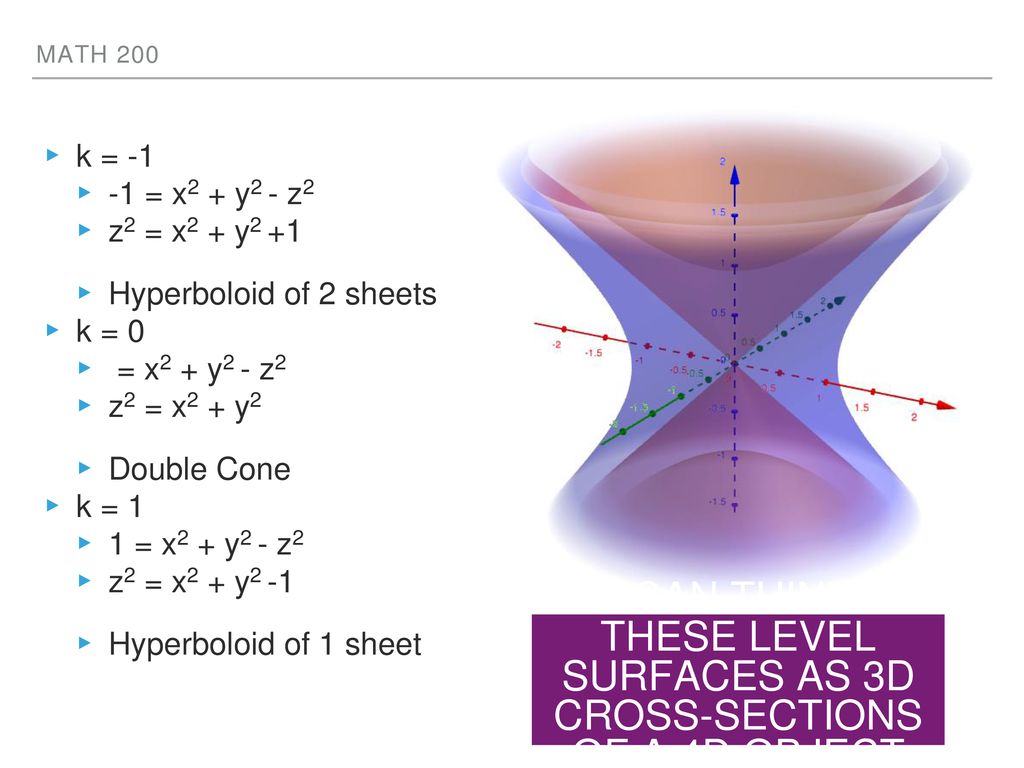



Functions Of Several Variables Ppt Download



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf
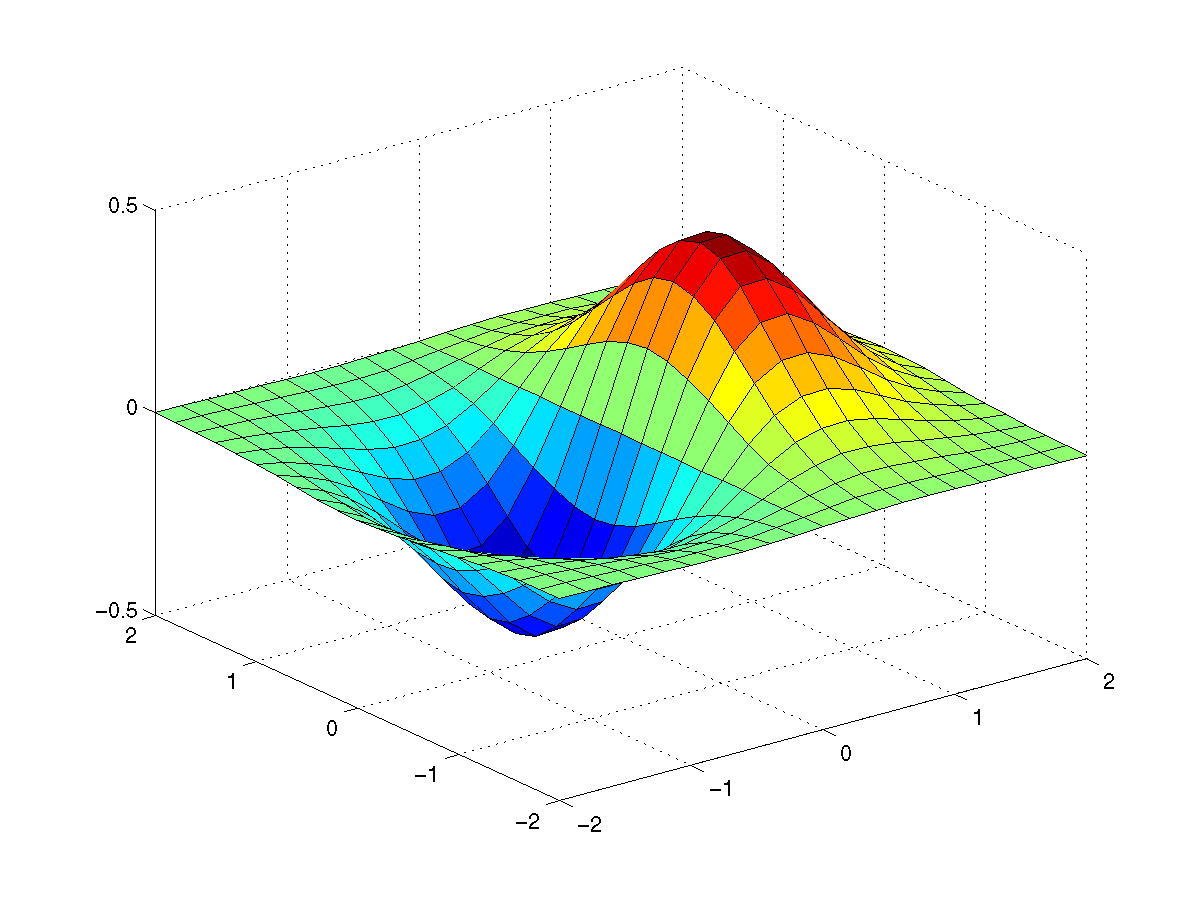



Matlab



70以上 Y2x2 Z2 ニスヌーピー 壁紙
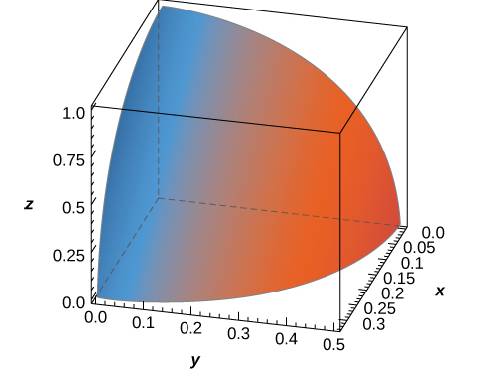



The Solid E Bounded By The Equation 9 X 2 4 Y 2 Z 2 1 And Located The First Octant Is Represented In The Following Figure A Trite




Graphs Of Surfaces Z F X Y Contour Curves Continuity And Limits




Matlab Tutorial



0 件のコメント:
コメントを投稿